※本ページにはプロモーションが含まれています。
しばらく間が空いてしまいました。すみません。新しい研究を2つ同時に走らせようとして、調べ物と実験づくりをやっておりました。
さて、思い出していただきたいのですが、このセルフ連載の目的は「IATの結果をBayesian hierarchical diffusion modelを使って分析すること」です。データとモデルを照らし合わせて、IATでの結果(反応時間)がどのようにして生成されたのかを理解したいです。
そしてこれまでは、IATとは何なのか、diffusion modelとは何なのかを(ザックリとではありますが)紹介してきました。なので今回は、「Bayesian hierarchical」の部分についてお話ししようと思います。
今回の話を書く上で、StanとRでベイズ統計モデリング (Wonderful R) を参考にしました。通称アヒル本ですね。いつもお世話になっております。
ベイズって何?
まずは「Bayesian hierarchical」の内の「Bayesian」について見ていきます。ここで言うベイズ(Bayes)は「ベイズ統計」のことを指します。トーマス・ベイズが提案したベイズの定理を基にした考え方のことです。では、「ベイズの定理を基にした考え方」とはどのようなものなのでしょうか?
ベイズの定理は、データを得ることによって知識が更新されていくことを表現しています。
上の数式のp( θ )は事象θが起こる確率、p( y )は事象yが起こる確率、p( y | θ )は事象θが起こったときに事象yが起こる条件つき確率、p( θ | y )は事象yが起こったときに事象θが起こる条件つき確率を意味します。
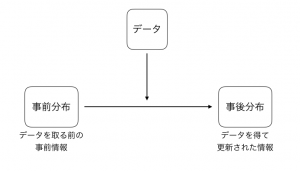
この事象θを、「事象yが生じる原因・背景」とすると、p( θ )は事象(y)が起こる前の状態の確率:事前確率となります。そして、p( y )は結果、p( y | θ )は原因があったときに結果が起こる確率、p( θ | y )は結果が起こったときに原因があった確率:事後確率となります。ベイズの定理が求めるのは、事後確率(データを得て、事前確率の状態からから更新された情報)です。
ここまでで登場している「確率」は、何か決まった1点ではなく、確率分布を想定しています。ここが従来の統計学とは異なる、ベイズ統計学の考え方の大きなポイントの1つです。なので、強調するために事前確率・事後確率というよりも、「事前分布」「事後分布」と呼ぶことが多いと思います(上の図でも「事前分布」「事後分布」と書いてあります)。
ちょっとよくわかんないという方は、こちらのスライドをご覧になるといいかなと思います。数式だけだとよくわかんないので、カープで例えてくださっています。具体的なイメージが掴めるはずです。私もこのスライドのおかげでベイズの雰囲気を掴むことができました。
階層って何?
次に「Bayesian hierarchical」の内の「hierarchical」について見ていきます。hierarchicalは「階層的な」という意味の形容詞ですね。モデルに階層性を持たせるというのは、どういうことなのでしょうか?
モデルに階層性を持たせることの狙いは、データが階層構造を持っている(と考えられる)場合に、その特徴を捉えたモデルを作ることです。モデルに階層構造を持たせるというのは、こういう感じのイメージです。
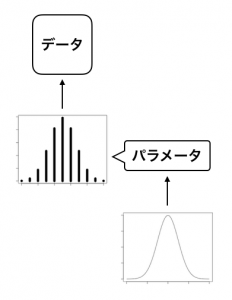
具体的な例を考えてみましょう。あなたは小学校の先生です。そして、あなたが受け持っている学年全体の算数の習熟度を確かめたいと思っています。そのために、10問からなるテストを実施しました。児童たちは一体何問正解することができるでしょうか。
正解できた数はカウントデータなので、児童が何問正解できるかは二項分布に従うと考えられます。この二項分布の位置・形を決めるパラメータ(=正解できる確率)をθ([ 0, 1 ]の範囲の実数)とします。
どの児童も同じ正答率になると予測できるなら、そのまま推定を始めても良いのですが、児童の中には算数が得意な子もいれば、苦手な子もいるでしょう。このことから、児童がテストで正解できる確率を考える上で、個人差を考慮する必要がありそうです。
クラスごとの違いをモデル化するために、得られたデータをクラスという要因でグループ化(階層化)します。例えば、児童の正解率を説明するであろう二項分布のパラメータθ(得点率)が、正規分布に従うとみなします。このように、データを説明する確率分布(今回の場合は二項分布)のパラメータを予測する確率分布(例えば正規分布)を設定することが、「モデルに階層構造を持たせている」という状態です。これによって、個人差やグループの差を考慮することができるようになります。やったね。
モデルに階層構造を持たせた具体例は『StanとRでベイズ統計モデリング (Wonderful R) 』のChapter 8をご覧ください。あと、Chapter 6にはいろんな確率分布の説明が載っています。また、『ベイズ統計で実践モデリング: 認知モデルのトレーニング』(通称「怖い本」)にも、階層構造のあるモデルの話が載っています。
階層ベイズモデリングはIATの分析になぜ良いの?
さて、ベイズと階層性の話をしたところで、今回のタイトルにもある「階層ベイズモデリングはIATの分析になぜ良いのか」を説明していきたいと思います。
IATは潜在的認知の個人差を測定するための指標だと考えられています(潮村, 2016)。なので、diffusion modelを用いてIAT課題での反応時間の生成メカニズムをモデリングする際、個人差をモデルに組み込む方が良さげです。これを実現するために、モデルに階層構造を持たせます。モデルに個人を単位にした階層構造を持たせることで、個人差をモデル化することができます。
パラメータを確率分布だと仮定してモデルを階層化すると、従来の方法(最尤推定)では解けなくなってしまうことがあります(計算がめちゃくちゃ難しいらしい)。この問題点を解決する方法の一つがベイズ推定とマルコフ連鎖モンテカルロ法(MCMC)というやつです。MCMCの話をしだすと長くなるので、気になる方は『StanとRでベイズ統計モデリング (Wonderful R) 』のChapter 2(12ページ)をご覧ください。
以上の理由から、IATをdiffusion modelで分析する際、階層ベイズモデリングを用いるのが良いんじゃないかと思います。
次回はdiffusion modelを階層ベイズモデリングでやる話を書いた、Vandekerckhove et al (2011)の紹介をしようと思います。
今回の記事を書く上で、いつもお世話になっている先輩の武藤さんにご意見をいただきました。ありがとうございました!